本讲内容难度适中，按顺序本应在链之后讲解，但为便于用链解释fish而提前安排，对我来说是一次较为轻松的讲述。

当一个数独中某候选数存在两条强链，且它们的一端位于同一行、列或宫时，另一端的公共影响格可被排除，这实际上体现了弱链接的作用。

这是一个典型的强弱强链结构，同一单元内的两个相同候选数构成弱链接，其余两段为强链接，两端点间形成强关系，因此可排除其共同影响区域中的该候选数。

1. 摩天楼（Skyscraper）

有了之前的基础，这个就容易理解了。无需多言，画个链条即可说明。同样，该模型也可在一侧连接区块，形成类似区块摩天楼的结构，就像之前提到的带鱼鳞状的X-Wing一样。

2.1双线风筝（2-String Kite）

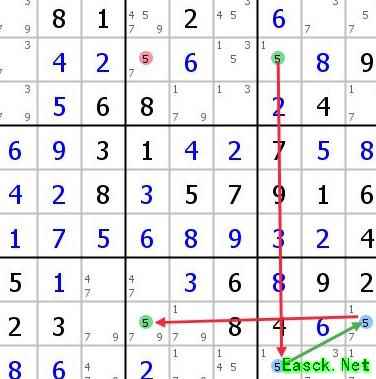
我向来不刻意区分这些手法，归根结底都是强弱交替的链条运作。

双线风筝，又称双重双线风筝，通过两条控制线实现灵活飞行与精准操控。

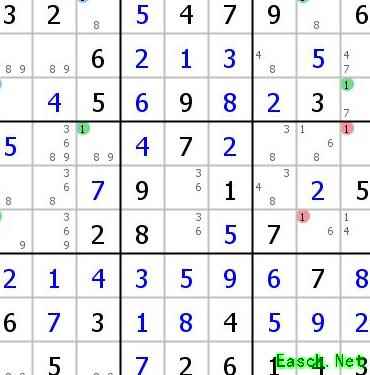
无需画链条，只是两个双线风筝简单组合，可分别独立分析，合并后也无法额外排除其他格中的候选数。

3. 多宝鱼（Turbot Fish）

多宝鱼并非鱼类，X-Wing亦非机翼，名称中的字眼常具误导性，实则与其表面含义大相径庭，需透过现象看本质。

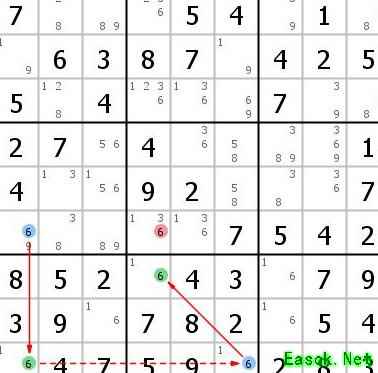
因此，我认为区分这些技巧作用不大，若非得找出差异，仅在于链的形态：第一个为直—直—直，第二个是直—弯—直，第三个则是直—直—弯。

4.1 空矩形（Empty Rectangle）

空矩形本质上是区块中的双强链结构，仅在形态上呈现为矩形。

将c6r46视为一个整体，相当于一个包含数字9的区块，此前举例时已作说明。该区块与r4c5中的候选数9形成强链关系，因为在宫b5中，若9不在该区块内，则必位于r4c5。由此构成强—弱—强的推理结构。需注意，该区块的作用范围仅限于宫b5和列c6，因此其他区域如r8c5的候选数9不能被删除。尽管表面上看b5中其他蓝色标注的9似乎也能与c5产生关联，但必须明确：此链的起点是特定区块，而非b5中所有含9的单元格。

提供一个示例，供你练习绘画，两种方法均可尝试。

有两个候选人的选举实例无需赘述，换个角度看其实就是多宝鱼现象。

4.2双空矩形（Dual Empty Rectangle）

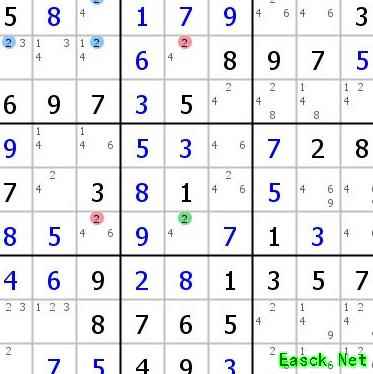
这个例子若用链式解释显得不便，不妨直接假设，实际上完全可行。

假设b1中某个格子填入2（因b1必含一个2），则无论哪种情况，r6c3与r2c5均不能为2。这是由于它们分别与r6c5形成强关系：若其中任一格非2，则r6c5必为2。而若r6c5也不为2，则需r6c3和r2c5同时为2，但这将导致b1中无处可填2，矛盾。

两条链相互交织，各自删除的部分恰好构成链的组成部分。

这种情况较为特殊，共轭点r6c5必为2，形成双空矩形，无需进行删减候选数操作，尤其在具备自动清除功能的应用中更为明显。

习题1：

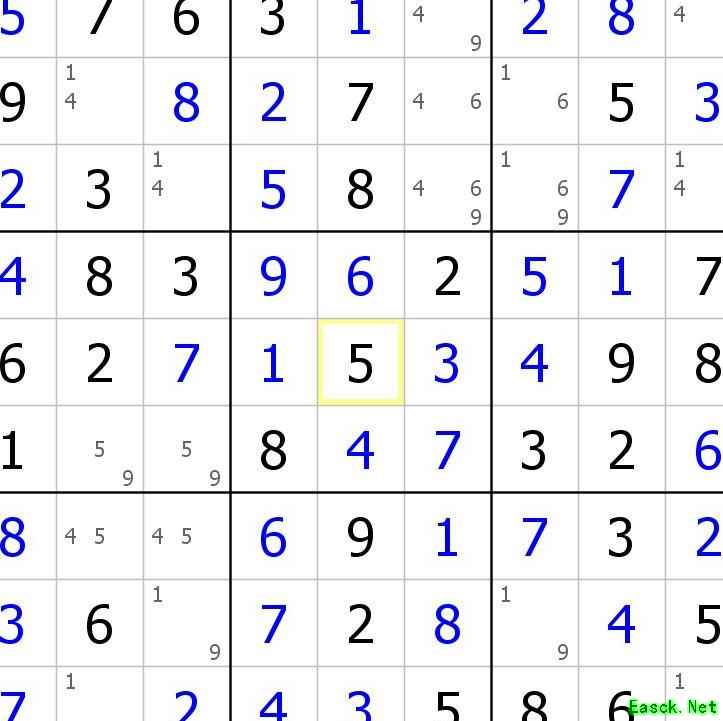
寻找有效的双强链以排除候选数。

习题2：

寻找有效的双强链以消除候选数。

这一讲看似简单，实则建立在前文基础上，因未作过多解释，需结合之前内容理解。

答案在回复中，附有总集篇链接，若我未记错的话。

小灰数独入门精讲合集