1.简单着色（Simple Colors）

简单颜色法只用两种颜色标记，从仅有两个候选数的格子出发，沿着共轭关系不断着色，直至无法继续。最终可能出现两种相互矛盾的情形之一，从而帮助排除错误选项或确定正确数字。

当某个无色单元格位于两个异色单元格的共同影响范围内时，由于同色单元格要么全真要么全假，这两个异色单元格中必有一个为真，因此该无色单元格中与之相同的候选数可被排除。此逻辑类似于链结构中两端点共同作用区域的候选数删除。

当两个同色单元格位于同一行、列或宫内时，根据染色法原理，这些单元格要么全为真，要么全为假。但由于在同一行、列或宫中不可能出现两个相同数字，故它们同时为真的情况不成立，因此这些同色单元格必须全为假。

不懂就看粒子，直观易懂。

我先来展示一下如何绘制此图。

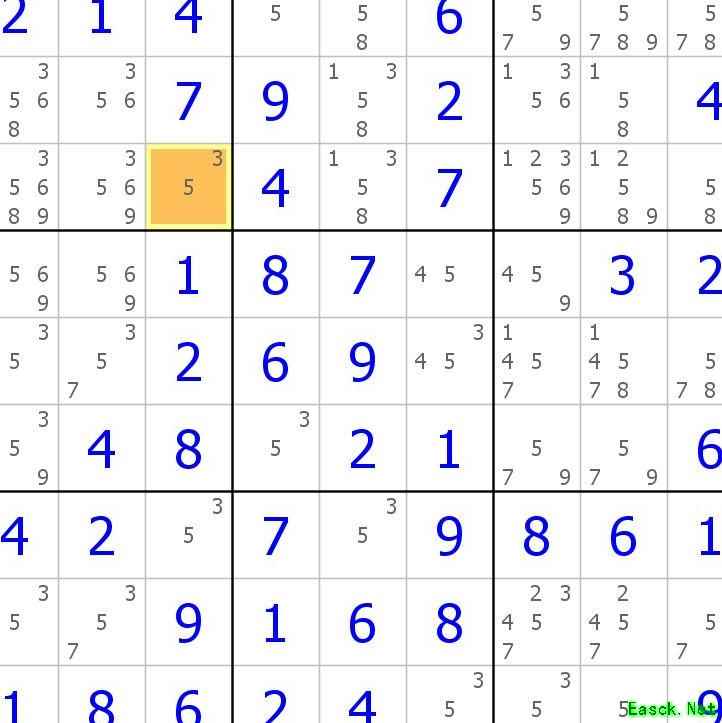
首先选取一个起始格，通常选择只含两个候选数且结构简单的格子，本方法仅针对单一候选数进行分析（例如本文以数字3为例）。接着，寻找与该格处于同一行、列或宫，并且在该行、列、宫中候选数3恰好只出现两次的其他格子，这些位置构成强关系链，需用不同颜色加以标记，以便后续推理识别。

从该格出发继续寻找符合前述关系的格子（如R7C5），需交替使用两种颜色，即强弱交替进行，直至无法再找到符合条件的格子为止。

只需关注候选数3，忽略其他数字，起点有两个候选数即可，其余无需考虑。

此例仅涉及前述第一种情形，即颜色陷阱。所有标红的候选数均可删除，因为它们位于行、列或宫内同时存在两种颜色格的交叉位置。例如R8C1，其所在列有深色格，所在宫和行则有浅色格。回顾之前的链式逻辑，这本质上是强链与弱链连接后，两端强节点共同影响区域的结果。这种表现形式更为直观，相比记忆复杂的链结构，更便于观察和运用。

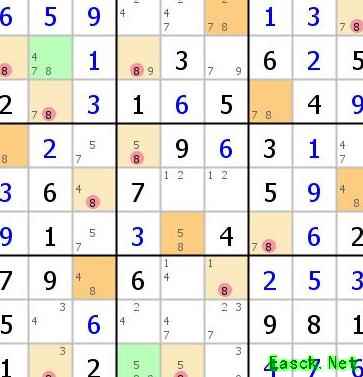
在此例中，我们将不参与该逻辑关系但包含候选数8的单元格用绿色标出，以便区分，不再重新绘图。本例属于第二种情形，即色块矛盾（Color Wrap）。此时可将红色标记的候选数删除。这些被删去的格子均出现在同一行、列或宫内，并且含有两个或以上的同色格。由于同色格之间具有共真共假的性质——若通过强链连接，则第一个格为8时，第二个必不为8，第三个又必须为8，因此奇数位格状态一致，形成同色。当同一行、列或宫中出现两个同色格时，若同时为真，便会导致该区域出现两个8，违背数独规则。因此，它们不能同时成立，只能全部为假，故可安全移除这些红色候选数。

我觉得挺有趣。

2. 多彩着色（Multi Colors）

多彩着色指用多种颜色进行标记，着色完成后，会出现两种可能引发消除的情形。

当同一宫内存在两个不同颜色的有色单元（构成弱链）时，因它们同属一个宫，无法同时为真。由此可知，第一个颜色的反色或第二个颜色的反色中至少有一个必须成立。因此，在行、列或宫中，若某候选数出现在至少两个具有这两个反色的格子中，则该候选数可被排除。

若两个同色单元格（如颜色1）处于同一行、列或宫内，且存在另一对异色单元格互为对立关系，则该异色对中必有一个为真，从而导致颜色1的单元格中至少一个为假。由于同色单元格在对应候选数的真假状态上保持一致，因此颜色1的所有单元格均不能成立，对应候选数可从这些单元格中排除。

难以理解？请看下面的例子来帮助说明。

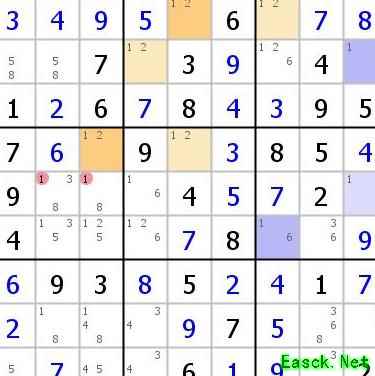
此前我们已学会用单一颜色标注，现在另选一个起点，采用不同颜色进行标记，仍需遵循相同规则。注意颜色深浅交替使用，最终呈现所示的结果（可自行绘制，此处候选数为1）。

此情形符合前述第一种情况。注意观察b3区域，其中存在两个不同颜色的格子位于同一宫内，它们构成弱链关系。需牢记这两个格子在颜色上的深浅差异。本例中，这两个格子呈现一深一浅的状态（但并非绝对，也可能同深或同浅）。由于它们共处一宫，因此不可能同时为真。这意味着各自对应颜色体系中的另一个格子必有一个为真。例如，若R1C7与R2C9中至少一个为假，则其对应颜色的R1C5与R5C9中至少一个为真。基于这一逻辑，若能在同一行、列或宫中发现一对颜色不同且深浅相异的格子，则它们共同影响的单元格中的候选数可被排除。这种关系即为强链关系，可自行标注验证。如本例中R4C3与R5C9之间即形成强链，它们共同作用于以红色标记的交集格，这些格中的相关候选数即可删去。

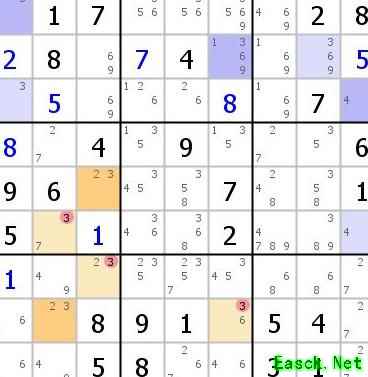
图的绘制方法暂不赘述，此处对应前文提到的第二种情形（候选数为3）。将浅黄色标记为A1，深黄色为A2，浅紫色为B1，深紫色为B2，便于后续区分与分析。

观察发现，颜色A1所在的R6C2格与同行为颜色B1的格相连，而颜色A1的另一格R8C6则与同列为颜色B2的格相关。由于同一颜色中不同深浅的两个格构成强链，二者必有一真。无论哪一个为真，都会与颜色A1所在格处于同行、同列或同宫，导致该颜色A1中的某格必然为假。而同一颜色且深浅相同的格在逻辑上共存共亡，因此一旦其中一格不成立，整个颜色A1的所有格均不成立。

这种方法其实还有一些实用技巧，可惜我未能完全掌握，因为使用的人实在太少。初学者往往不了解，而进阶玩家通常直接用更高效的链式操作完成任务，省时省力，且许多应用并不支持此功能。尽管如此，我依然乐于探索其中的乐趣。

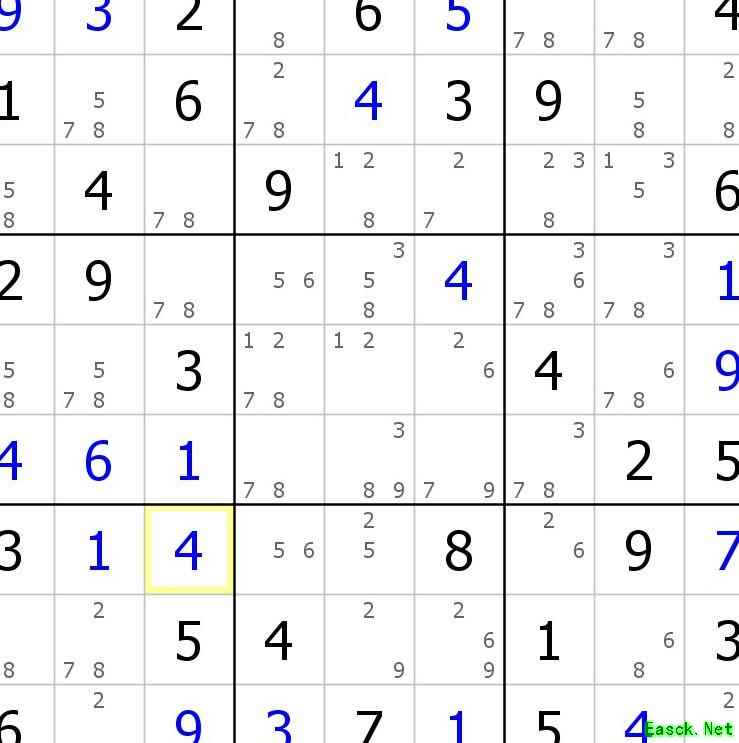
出个题吧，候选数为2

答案在回复中，附有总集篇链接。

小灰数独入门精讲合集